串联和并联电容器

电容串联

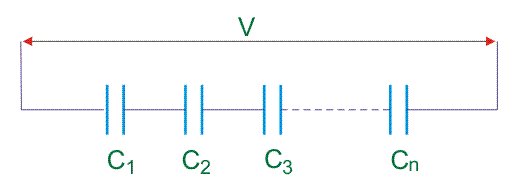
让我们连接n次数电容器系列．V伏适用于这个串联电容器组合。

让我们考虑电容电容器是C₁C₂C_3.C……_n分别和电容器的串联组合的等效电容为C.电压滴在电容器被认为是V₁, V₂, V_3....... .v._n,分别。

现在，如果Q库仑是通过这些电容器从源传递过来的电荷，

由于在每个电容器和I整个串联电容器组合中积累的电荷是相同的，因此我们认为是Q。
方程(i)可以写成，

并联电容器

电容器被设计成以电场的形式储存能量，即静电能。当需要增加更多的静电储能容量时，需要合适的增加电容的电容器。电容器由两块平行连接的金属板组成，并由玻璃、云母、陶瓷等介质隔开。该介质在两极板之间提供了一种不导电介质，并且具有独特的保持电荷的能力，而电容器存储电荷的能力被定义为电容器的电容。当一个电压源通过电容器的极板连接，一个极板上的正电荷和另一个极板上的负电荷被沉积下来。累计电荷量q与电压源V成正比，

式中，C为比例常数，即电容。它的价值取决于电容器的物理尺寸。

式中，ε =介电常数，A =有效极板面积，d =极板间距。

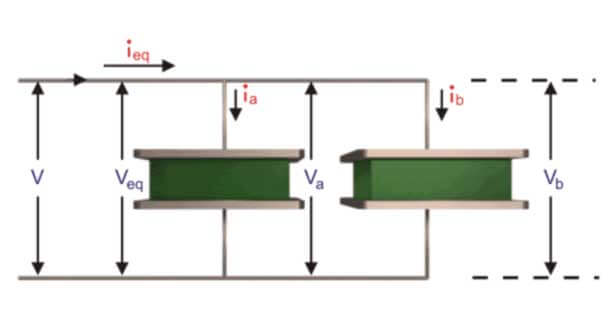
增加一个或两个以上电容器的电容值电容器是并联的当两个相似的极板连接在一起时，它们之间的有效重叠面积以恒定的间距相加，因此它们的等效电容值变为单个电容的两倍(C∝A)。电容器组用于各种制造和加工行业，并联电容器，因此，通过调节并联电容器的连接来提供所需的电容，从而有效地利用它作为电力系统补偿中无功平衡的静态补偿器。当两个电容器并联时，每个电容器的电压(V)相同，即(V_情商= V_一个= V_b)和当前(I_情商)分为两部分_一个和我_b．众所周知
将方程(1)中的q值代入上式，

后一项变为零(因为电容器的电容是常数)。因此,

申请Kirchhoff的现行法律在平行连接的输入节点


最后我们得到了,

因此，当n个电容器并联时，整个连接的等效电容用如下公式表示，该公式类似于串联时电阻的等效电阻。

并联电容器等效电容表达式的求法

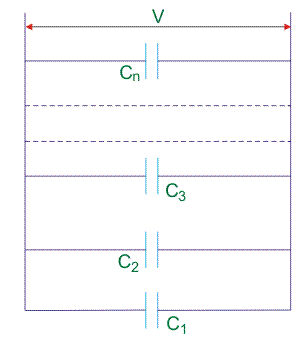
让我们连接n次数并联电容器,在一个电压源V的伏特。

让我们考虑电容器的电容为C₁C₂C_3.C…_n分别和电容器组合的等效电容为C.作为电容器是并联的就像每个电容器中的电流是一样的。并联组合的总电荷，将根据其电容值划分到每个电容器中，但每个电容器的电压是相同的，在稳定状态下，它完全等于应用的电压电压．

在哪里，Q.₁,问₂,问_3.,……问_n电容C的电荷是多少₁C₂C_3.．．．．．C_n分别。

现在公式（2）可以写成，